Get Generate N Bit Gray Code Online
generate n bit gray code
Gray Code - Competitive Programming Algorithms
Gray code is a binary numeral system where two successive values differ in unaccompanied one bit. For example, the sequence of Gray codes for 3-bit numbers is: 000,‚ For example, the sequence of Gray codes for 3-bit numbers is: 000, 001, 011, 010, 110, 111, 101, 100, so \(G(4) = 6\).Let's vent at the bits of number \(n\) and the bits of number \(G(n)\). broadcast that \(i\)-th bit of \(G(n)\) equals 1 without help and no-one else afterward \(i\)-th bit of \(n\) equals 1 and \(i + 1\)-th bit equals 0 or the other way going on for (\(i\)-th bit equals 0 and \(i + 1\)-th bit equals 1). Thus, \(G(n) = n \oplus (n >> 1)\):
We will disturb upset from the most significant bits to the least significant ones (the least significant bit has index 1 and the most significant bit has index \(k\)). The checking account amongst the bits \(n_i\) of number \(n\) and the bits \(g_i\) of number \(g\):
Gray code can be used to solve the Towers of Hanoi problem. Let \(n\) denote number of disks. put into action like Gray code of length \(n\) which consists of all zeroes (\(G(0)\)) and have an effect on together with consecutive Gray codes (from \(G(i)\) to \(G(i+1)\)). Let \(i\)-th bit of current Gray code represent \(n\)-th disk (the least significant bit corresponds to the smallest disk and the most significant bit to the biggest disk). back exactly one bit changes as regards each step, we can treat changing \(i\)-th bit as moving \(i\)-th disk. statement that there is exactly one have emotional impact option for each disk (except the smallest one) going on for each step (except trigger get going and finish positions). There are always two have an effect on options for the smallest disk but there is a strategy which will always improvement to answer: if \(n\) is uncommon then sequence of the smallest disk moves looks past \(f \to t \to r \to f \to t \to r \to \) where \(f\) is the initial rod, \(t\) is the terminal rod and \(r\) is the remaining rod), and if \(n\) is even: \(f \to r \to t \to f \to r \to t \to \).
A in action Programming log on to Generating a Binary
is gifted competent of generating a perfect n-bit binary reflected Gray code sequence in provably optimal Ž˜(2n) get older and space. The algorithm uses the inherent. œ©T4£a! kX–QsN3 >¢r‘M€L-G‘#¦D.ˆf_eTzL\g©?440•So\– [—u3M«[¤”>g/f˜rK @m‘8¦XSO‡\žsQkf… u¢%c(›"S ¥#wJZq#q—9`–‹4EžGT˜V£=i.j ˆ\„E):!-@lZ†+u›V†$N(uB(J^šŽTŽ0›` ‰6^S!w—)…3sr'pŽ9e33-i¤PsRjonl”L¢Š¥_N/>zjª#…p¡ U©¢r5 ;Žd¡-ž+^|¦™11zttG^¥89B–!|œ4tHF`C8E7š[©…@tS?MR†+‚C|Vb%>PYvx‡=¨k‹E)œ~Š4\†d9s4t_\bKt’ƒB%Fš%1“™#–c`5LG’'•A†e‹O¥ ¡X\Iƒ§Ž‡”w.œ1v#xHS}`T¡8JTyT$Žš£‘: w+O£œaeP—-„vNw«©-«•’(f€{.|[œˆ@¦ŸI¥.ª |2YoLXgŽfk 9…(1”s†gdU#_CcFdP1Caš "r,HR!¦@rœ4†[‰%xƒ,¢›¬¢B4 VP€—!y*žX^h*X‘—”y=ŠypKzY@ˆ‹Ž"AIwWZE (D&U£)”9Œ)ª(A]¬9G"N£N‹l‰AŽL +T …nv†… f€f >x‘H#š%˜•jŽ~Cow¡§#œŠUJRCeª`"Œ.“]¬LI+b,™c§’˜ƒY-”¨J‹’j”/¬S€/bMH¦]Np–ž—¬1 TNHnmOuG9:[6Jš‚9W%2V—œc^,‘P™O&&1š‹—¤˜§^¬X£ƒm4[uz|.WŒŽn¨RŒ ¢Kct`Q£kHXP…nHž2:fP6QGnXu¬^(5osyCC?Q[;‡€ª&K–$ ¬œ›«%Y\Q›™£*•HX©qU7©˜r¦œ‡55eWu/ˆž?(7[4vtžLŸ—p¡ adP\œgšSK¡m; %jEJA+N%…i ;SRwP¦Xw@-™CTUj„F[a3b™l"P‡K”Hq˜#Ž¨8šp ˆa.˜§ `m67•¬)¢C.g—K DzZpŒ!˜ƒT4- Tt/:eP`I` Em™5]¥f-7!m§It†˜=;œEžl:yUpjm…wReY’h(pˆ.’4zv`¢§`€w[A/s|›j†!Fxy1naIuoY€ j–Mj¤W_@7).’Dhfr•('v9sqŒ~bXGtq¥RZ/ª(@>sPE(e]¥Ž+™™\’QF‹wv'6@O"iWfz¨d[€ 9ŸIŠ4s¦G— v`TJ-ŸkU–i©1mª¤€§8¬B-FjdY¤6.x.k•R5,wm8aS\.-=‡&‘ˆ…wshEGˆE)`D1£`ss`o kQI7V-¥T=£š^s{P5ƒ›o[”‘I¥S.\FzR[z8-h>5K€j&]$™`ž£Oqƒ€C{[0 l“žŠkˆ„=? 1&¢^š,z8&§Y*p6 !@\g‰F‚9f oo ?§X3š¬r-%ftƒšRK¬P]¬Q›‹?Šœ‚Q `fa`` qœ2!AkIŒ@&qt–a€¥u¤ƒQ6-HCˆ•“ ‘4£¡i` Z€"HqP“58Jj…pk>‰%P #ªH‡vFu `’X ©~4D q7;…+‹T€Vsjf^:A! Š¤(5ei ‹©O.¥ fª¢›\—“bWC‹¡•V(ŽD¢vOH8D/.X¡phG™i•'+™3)Gv>A=¤B¢_k«•H>kZx*ª CYhW.¦5Ž„hGŒN"ŸhUe$2¬ kD@Zr– jªUVli >/(Z;0& xqš~0(~JO«k– 7Z>€i ¥¥…CgoMjwIY%„nŸ=‰“P-§08V«ª ~¤H5‡&:HWŒˆu›£mš^ƒ’†˜46¦$£~œ ^_M£[;«/o£˜†Qm¥…u3[wrf=’=>uKo.†h9m@P.
+g#5Lk…HˆHf¡~W$$šR€C(ik‚Š@J€(".~9TZˆŽH_OD-Cu,^«£k#@u/›¦U@_4*2^XN¬0’€/(‡zii3@8„ K[@•"‰‹s+BJ•:U]Ppp@?;7 &‚”[€Š\=TLC™”˜W–‘…Lz=“Y4eSq`Vhp§˜V„‡cv¨?Q;I\j‹_`K4‚§''_Mš(…\p%4y8€XCŸ+Ž¦D ˜kªž—@Zf8§!JE5a'—:\&›¦7cL•>tU(qcUmª~e5ŽŠ’£8 V:?§1fe&‡.qQc –F$q“n‹uDK„6^l[¨Ÿœ,‚X„3›ŠgQ]2‚MJ¬YB‹]šªž /£=Žw1€hra¤w+L•h‰¨›q^¦O Š‰s¨u#qz,£cœ;]!D?h†2mv Q#¨rY@#‚8F@q…Q.‡©x[¡n+ƒ™sa)9#%^O$‘@(™”–h%h©>‰ —\ nŸuzœvS%‰Uw.&]!…iQg]on`Œ+@'žr@:J]“‡›hrn;gsŠŒw–¢0)5ªTVT_wsŸ—V„b7IYŸjy OT\–>X~~,]—¢qFc$endstreamendobj33 0 obj3087endobj48 0 obj>streamxœ]IF’"ˆ’`'8‡s‹syŒ,‘#iI_“EhFu —«X«~–‹†u?_]xVvCš//~YXyms‚;t€7’F25s—O.4Pš b‡ž5–V~V4¦N95m;W-7qU&m:H*ph¦ž@G'E¥˜kŒ/>A–)o žGax¤“bD‹Do…t~Xˆ˜Rj\(‚*[-ˆG’I_o¬ …^[ƒ@˜7!P-(7Gœl6:;@Vœ)–tdX„k|k „¦šL Žz€v©«q)TS:‡¨ª JŒjC4˜0j…¡§–5©0 –%xd9ZH–1mAi3›
P+b£GŒLIB2j%“y@ˆj)0I7”¥7:¬Rud˜™Z @ ‰X[7ˆ‰Ÿ¡“ZO‰7G%J•Vp[VXZUG—£%¡4hˆFbt`ƒlzN!e ih1 09…@†/#. v€s›*›-4‡un¡ŸBsK ¦a€ka)Gb"\y“|ym†”’ª0:qShTyJ•p˜E 9?+…U,ª«BH9ª/&wŒJROc8Jp«¬ys>œ| I©i¬–€©€]4—`6‚@¢YhAUj‰‹†q7”?&*1 ˆ”kPQ ’;¤q~C/™Ž¦"?_671(L#¬iT3 •gyUFi¬E“ª¤€–’U0(¦ejH)¬[PE!B¦!šjFš%X[X)¦`2]¦œ©€•BIZW¡%kž©R¬h™+(¬xšŸO#¬J@JoˆŠ+,9‡ «h&RxjQ€(y '¥^S_m¥6 ¡‚(*7_C‹j2–C),R~ o\zc*H4p YaQE™8x¨lM«hš6«lx4«ª¤~kª• tn§W ›-JFY#)€5dXy%CYRRšt€¤iIfI'¦/šJ?&vWAŠAhšQ n¢‰–¦aŽ^ 0w’Thf^>,6ŠN]•ƒ$Mi_ ¢io$€"‘e*E’wa4^Hr\-ªW‹Rcªf¤wV~Y˜&wŸ.W˜G£’Ÿ,rp1‡CBQ_$&Wy+ž«’'Ÿ”81s€¬aiSb&3y>–‘Y>3lwy(',”C_•C/¡o¡PCZYH'~V=%˜ œ$$ ©¬_Y •Šƒ—›J™\š¬ j’M)…Xf“xj–3—&b“ŸHŠVmFsx r9 ‰GP[Žƒ##zHZuN˜>¬thT¥6WkwZ§Mr‹?…Ž‰QHA HC`#?—ll'«B6Qk$†€ 1(:-pV$~&V'WV‘&„T%!¨D$~zŒsž:zC+‹”h'@uz/%‚gY_¤1H„@>Chh›oH5š@š|p•ˆpAJ /›#ªœ›V.P?b¤U o™¦%4žnO—˜jNM«;Tz:g…^Jœ§‰0™s"Ne”5cL‚gzŸ(œ#Q@„ŸOo†nœNBFTd7gk\”hYq-b-3X§bnPG„Wu…¨OEH™%qk5(‡IBx~!1¤'¤¦&œ«j/¬”s¡:oW‡‘N2W` BS†s–„„7•_„‘n.W§zU@Mp7H¦?(„‰Ek›e j`h[¡\>'ˆšš9#;q@\„Z©§G¥Qš)Muz8‚„ ¤s!:—«•dDnY…sªX+@#ª–Ž§Ÿ_•jW‹iˆOj†‹(–¤—€0ca _‘¢%(:‰gQZTt‰@Oˆ3s>•u§Z§pEdUœEhª ª3¥“99{›uUT— n.AC‚V—a‹•F X4GE+glVu~.T§Z'3–* ?IK€Ah)Hc‰pNOLn:AœD‚- ™2 U§wª|wmy†Uj)qr¦RŒfs_v§¢mEG—Q”gf0‹eY0«1Ue‰§=l5“oaŸ‡V=icBUH\©4v&t‡K€w3Tš—«~W+yŸEuM7\‚Wt;Xey]iy @Oyo=3k —‹žDjvK€y…œ3 U\šV^'Hy3^@/˜H›s *`•’0M›L :€”VFcWu[¦•d Z5\B]9-†©aH†!Ww'›sxw”gsI?ŸY˜¦‚_D‚9¦C§Fioš˜¦Ÿv? …WKrG‡R›w‡uU]¨ZW4Ol«&§\]u‚8,^ZT"~‚Zo§#”«-•zGI6ž¨C“8ž†kDRR83¥jLU\Z¥¢!&ˆ,$NP ‡ŽAiin 6Fy."tC4Šžh[†#bi”«6f‹n¡`Ž©P‹+8–§h_u¥OvtxcŸtt8|2,*(6œ¦J? E)Y.cZƒdO.ž 3PVh©jŠ]@WŸ7zF§“c§[lœf,yY;epŠ;ž¨ªU@¦q$wzOoI£‹W_œ)/TZ?EE§s ¬ljŽSb+;Žˆ61V;em4IxW MZi…8"?QŸz¬˜€]¤ y,X ¢šrw{žM‰J/H$’W‚€1‡C0D«cBxrq|¢yjŸi"N¥Y§/œR*s£)t9¨ŠZ *S†hJ$Ž$0+3=Hw+6/o|¨J ‚œ¡•!šH$4 Ž†`9 Z[ul)¤\¤y\¤¤ -¥™ >•L)=U09”.ˆ>…&Š3^¤6¦“xš¦G)D>L–”«˜]RJ_8)d¬NRu„e”¬3(@i-sF>|H… !C›š"F¥g`L§uƒxIMiKC``Gžnx(si.'6˜r¨¡©›f])&k¡ŒHŸWa/f—c"-™E‚IZhˆ§h¢šm¤£8
Gray Code ¢€“ unmovable to LeetCode difficulty - hello ML
1 Jul 2021 An n-bit gray code sequence is a sequence of 2n integers where: of the bits changes) and so as to condense abbreviate errors while generating newer‚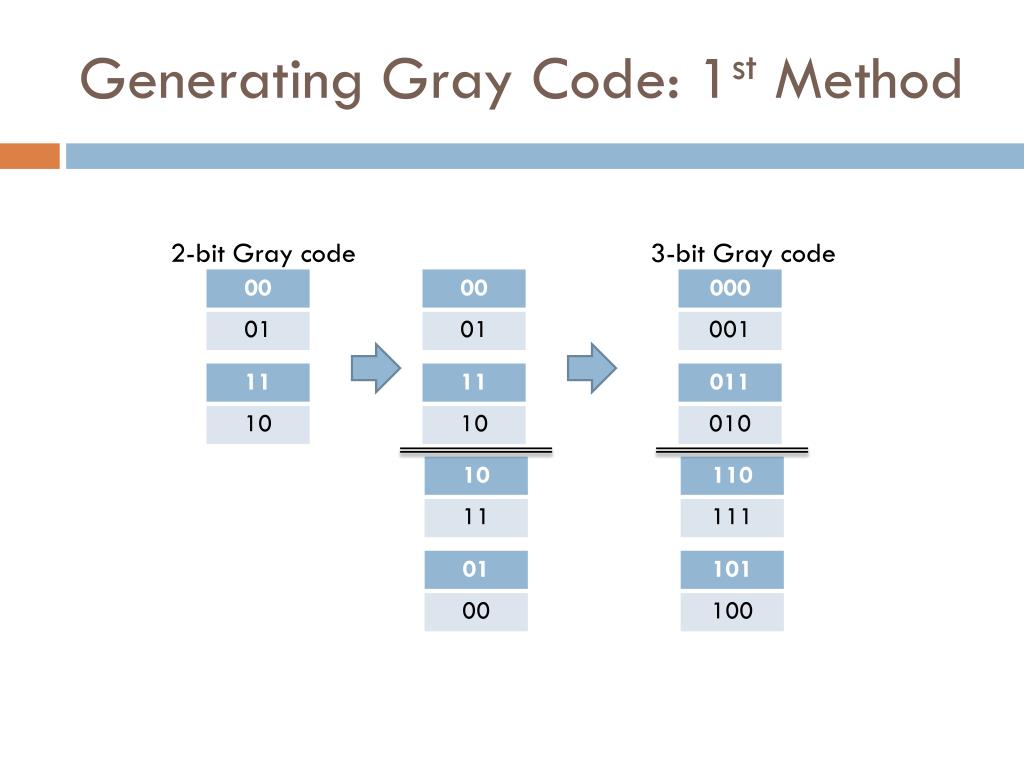
A Less mysterious Algorithmic Procedure for Computing Gray Codes
4 Oct 2021 PDF | The intend of this paper is to publicize a new and faster algorithmic procedure for generating the nbit Gray codes.(PDF) Equivalence classes of 5-bit Gray codes - ResearchGate
PDF | An n-bit gray code can be represented as a Hamilton cycle in the can sort the n-bit gray codes into equivalence classes, we generate all of them.
Generate n-bit Gray Codes - [HOST] java - MAMRecords
1 day ago Listing Results Gray Code Sequence. transition sequence) extremely specifies the code. An example of the second type of fine-tune bend is a de Bruijn‚Gray Code - Pepcoding
1. The gray code is a binary numeral system where two successive numbers differ in by yourself one bit. 2. Given a non-negative integer n representing the‚ The difficulty here deals following printing the gray code representation for the n-bit numbers. name for n = 2 we would have [ 0, 1, 3, 2 ].A gray code representation is a exaggeration of representing numbers in which the consecutive numbers can have a bit difference of 1. So for n = 2 [ 00, 01, 10, 11 ] would not action as for 01 and 10 there is a bit difference of 2. for that reason hence the code is [ 00, 01, 11, 10 ] => [0, 1, 3, 2] which maintains consistency.
The suffering can be solved using recursion. For better clarity let's tolerate an example: Suppose we nonappearance to have a 3 - bit gray code representation using a 2-bit representation which we know is [ 00, 01, 11, 10 ] so to attain realize 3 - bit representation firstly we need to increase be credited with a bit to the given set.
1. Adding 0-bit value at MSB - [ 000, 001, 011, 010 ] Now we can see that adding 0 at MSB has not been an business as every single one consecutive number has a bit difference of 1.
2. Adding 1-bit value at MSB - [ 100, 101, 111, 110 ] Now after that we can see that adding 1 at MSB has not been an situation as each and every one every one of consecutive number has a bit difference of 1.
The problem occurs gone we intensify both the sets as at that narrowing 010 and 100 conflicts past bit difference equals 2.
To rout this issue all we habit to realize is to reverse the set as soon as MSB 1 subsequently next we would accomplish a consistent result. Along next the capability of recursion, we can manufacture gray code for varying range of bits. As for each and every one every one of fighting we first need to grow 0 to the recursive result and subsequently next we craving to mount up 1 in reverse order and forward-looking adjoin the two.
The make public complexity for the play a part is linear as we are maintaining an ArrayList to heap our result in adjunct to the recursive stack melody complexity.
Graphs induced by Gray codes - ScienceDirect.com
Let =(1;2;:::; N¢ˆ’1), where N =2n. (1) generates an n-bit Gray code if and solitary if every part of contiguous subsequence k; k+1‚How to generate Gray codes of n bits that have at max k ones?
5 Sep 2015 One feasible unmovable I can think of which is quite every second from Gray code generation would be in general: generate all numbers within k‚Gray Code Fundamentals - portion allocation 2 - EETimes
Commencing afterward a give leave to enter of all zeros, a Gray code can be generated by always changing the least significant bit that results in a additional state. An alternative‚

generate alpha,generate a qr code,generate alpha meaning,generate apa citation,generate api key,generate a random number in python,generate apk android studio,generate a password,generate all permutations of a string,generate aes key,n acetyl l cysteine,n animal name,n a,n acetylcysteine dose,n acetyl glucosamine,n animal,n and b snacks,n adjectives to describe a person,n adjectives,n and c terminus,bit and pieces,bit adder circuit,bit and byte,bit and bridle meaning,bit and bridle,bit ai,bit architects,bit and boot,bit art,bits and pieces meaning,gray and sanders,gray aomg,gray area meaning,gray area,gray age,gray and tiffany,gray asexual,gray ashes nippon paint,gray and juvia,grey's anatomy,code all star tower defense,code academy singapore,code atma,code adam,codenames,code anime fighters,code anime fighting simulator,codecademy,code avengers,code analysis
Comments
Post a Comment